Accueil
Page personnelle de Thomas Briffard
Je suis actuellement consultant en ingénierie numérique, en portage salarial.
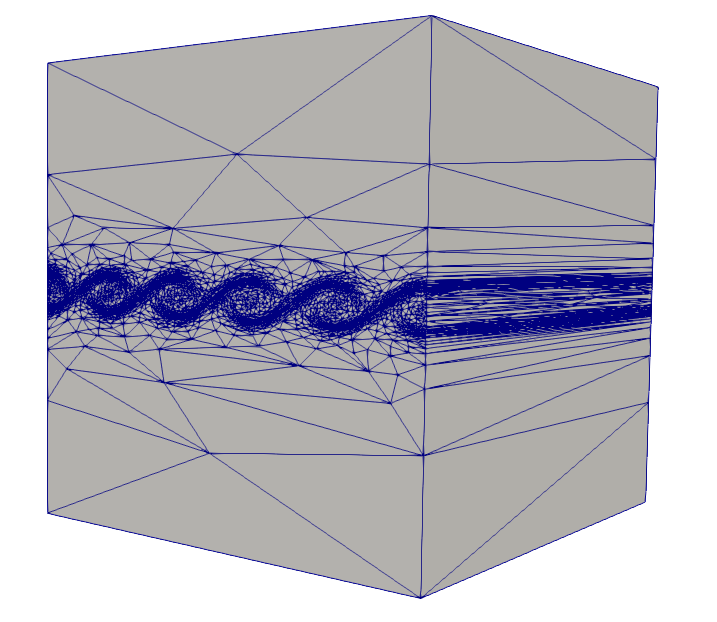
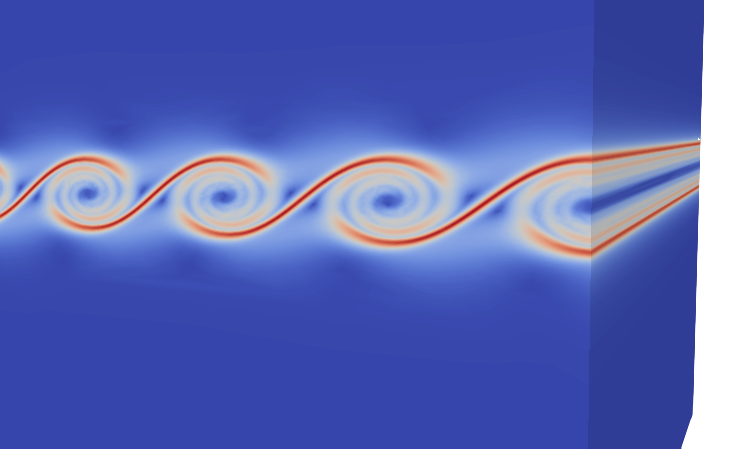
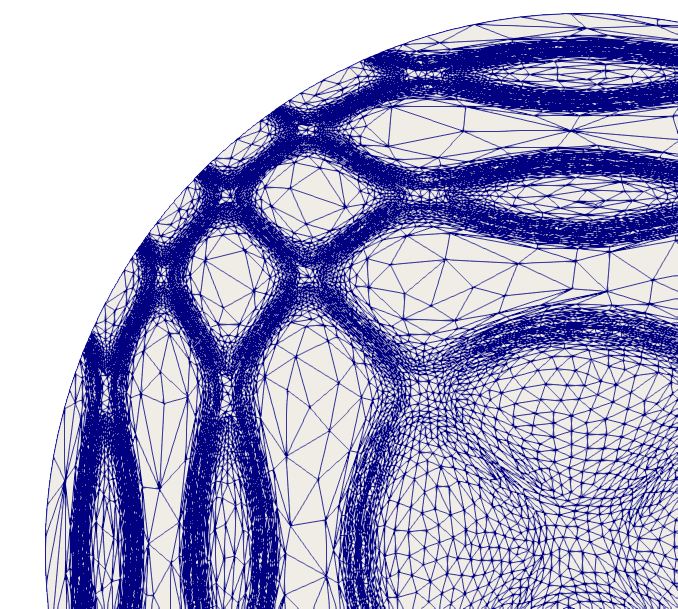
J'ai effectué mon doctorat en mathématiques appliquées au sein du GIREF (Groupe Interdisciplinaire de Recherche en Éléments Finis). Mon sujet de thèse portait sur l'adaptation de maillage, basé sur un estimateur d'erreur hiérarchique.
Ci-dessous, quelques résultats numériques avec adaptation de maillage.
Structure Lagrangienne Cohérente (SLC), convection Rayleigh-Bénard.
Curriculum Vitæ
Éducation
2013-2017
Doctorat en mathématiques appliquées
GIREF, Université Laval, Québec.Contributions à l'adaptation de maillage anisotrope sur base hiérarchique.
2012
Master 2 de mathématiques
Université Pierre et Marie Curie, ParisParcours Mathématiques pour l'entreprise (mention très bien)
Expérience
2020 - présent
Consultant en ingénierie numérique
Clermont-Ferrand, FranceConsultant en ingénierie numérique, mission effectuée en portage salarial (DTalents) auprès de la Manufacture Française des Pneumatiques Michelin.
2017-2020
Professionnel de recherche
GIREF, Université Laval, QuébecProfessionnel de recherche au sein du GIREF.
Hiver 2018, 2019, 2020
Chargé de cours
Université Laval, QuébecEnseignement du cours "Analyse Numérique pour Ingénieurs".
2013 - 2017
Auxiliaire d'enseignement
Université Laval, QuébecAuxiliaire au centre de dépannage et d'apprentissage, tâches de corrections d'examens, d'exercices en classe.
Mars 2012 - Octobre 2012
Stage de fin d'études
Manufacture Française des Pneumatiques Michelin, Clermont-FerrandValidation d'une chaîne de calcul par éléments finis.
Publications
- Y. Belhamadia, A. Fortin, T. Briffard (2019). A Two-dimensional Adaptive Remeshing Method for Solving Melting and Solidification Problems with Convection
- Dione, I., J. Deteix, T. Briffard, E. Chamberland, N. Doyon (2016). Improved Simulation of Electrodiffu- sion in the Node of Ranvier by Mesh Adaptation
- Fortin, A., T. Briffard, and A. Garon (2015). A more efficient anisotropic mesh adaptation for the computation of Lagrangian coherent structures
Enseignement
Analyse Numérique pour Ingénieurs (Hiver 2018, 2019, 2020)
Slides résumant la matière des différents chapitres : MAT-2910.pdf (contenu basé sur le livre du cours <<Analyse Numérique pour Ingénieurs>> d’André Fortin, 5e édition). Ces derniers contiennent des liens vers des fichiers Matlab (.m) téléchargeables et illustrant la matière.
Également disponible par chapitre :
- Chapitre 1 Analyse d’erreurs, développement de Taylor
- Chapitre 2 Équations non linéaires
- Chapitre 3 Résolution de systèmes d’équations algébriques
- Chapitre 5 Interpolation
- Chapitre 6 Intégration/Différentiation numérique
- Chapitre 7 Résolutions d’équations différentielles